In the previous post we looked into applying basic pattern matching with OpenCV to build a basic bot to play Burrito Bison browser game. However, there was very little game logic involved: it watched and waited for powerups to fill up, using them once filled up. Everything else was related to keeping the game flow going by dealing with menus.

In this post (or next few posts) let’s take a look at a slightly different game: Puzlogic. Puzlogic is somewhat similar to sudoku and comes with 15 different levels. The goal of the game is to place a set of given numbers into a grid where some cells are pre-filled with other numbers. The catch is that duplicates are not allowed in any column or row, and in some cases extra constraints can be applied, e.g. that numbers on a given column or row would add up to a specific sum.

I would recommend you to play the game for several rounds to familiarize with it.

But I think Puzlogic is a convenient problem to explore several approaches on:

1. More elaborate computer vision approaches to understand the grid, e.g. recognition of digits, identifying different elements (irregularly spaced grid, set of given numbers, sum constraints)
2. Solve the puzzle using Python, e.g. using a bruteforce approach, or using a theorem prover like Z3.
3. Lastly, combine the two components above and use the a mouse controller like Pynput to tie it all together.

In this first post let’s start with the puzzle solver first, tackling CV and controls portion in later posts.

Planning

Again, at first I’d recommend completing a first few puzzles manually to learn how the game works. But here are my first impressions:

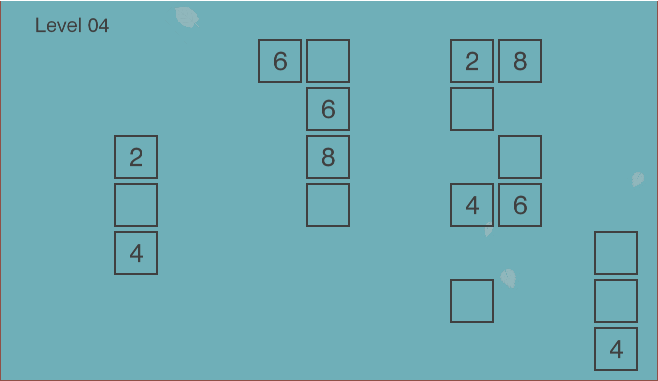
The game board is in the form of the grid. However, not every location in the grid is a valid cell - there may be spaces around valid cells. Some valid cells have pre-filled numbers in them which cannot be overwritten, while empty cells are intended for the player-controlled pieces.

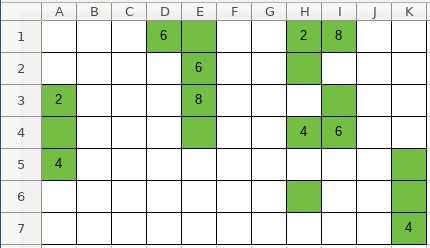
Since it is a grid, we can think about it as an NxM matrix, where N and M are distances between furthest horizontal and vertical valid cells. However, because most cells may not be valid, it would be a waste of space to represent it as a two-dimensional array. Instead it can be represented as a Sparse matrix using a coordinate list, where each cell is represented as (x_coordinate, y_coordinate, value) triplet. So the full grid would be represented as: [(x_0, y_0, value_0), (x_1, y_1, value_1), ... (x_n, y_n, value_n)].

Secondly, the numbers player has to use (we’ll call them “pieces”) are displayed near the bottom of the window in another grid, which means coordinates will be important later when moving the pieces to the game board. That can be represented as a simple list of integers: [piece_0, piece_1, ..., piece_n]

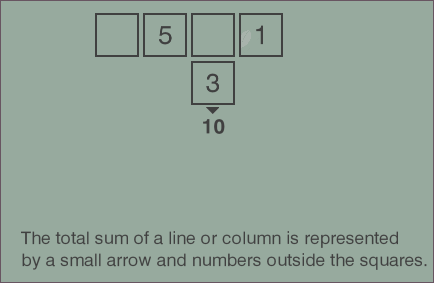
Third, if you play a few more rounds of the game, you’ll see how sum constraints are displayed. They can be applied to any row or any column. We can represent the constraint with another triplet: (index, 'column', target_sum) or (index, 'row', target_sum). The list of constraints then would be represented as: [(index_0, dimension_0, target_0), ..., (index_n, dimension_n, target_n)].

So we have our three parameters: grid, pieces and constraints.

And lastly, how would a solution be represented? The game is won once all the game pieces are moved to the game board, the game board is valid and all constraints are satisfied. So we could represent the solution as a list of moves, where a move is a triplet (x, y, piece), denoting on which coordinates each piece should be placed.

The number of pieces is low, the size of the game board is also small, so we can use a brute force depth-first search to find at least one solution.

Implementation

For pseudocode of the algorithm, I think a pattern I’ve seen used during Martin Odersky’s Scala classes works well here:

1. Generate all possible moves for the given position;
2. Filter the list of all moves leaving only the legal moves;
3. Recursively repeat from step 1 with the new game state.
4. If the solution is found - recursively return it through the execution tree, if not - allow the depth-first search to continue until the whole search space is exhausted.

Let’s start at the top with solution() and fill in the blanks:

    def solve(self, board, pieces, constraints=[]):
        if len(pieces) == 0:
            return []

        for (move, new_board, new_pieces, new_constraints) in self.legal_moves(board, pieces, constraints):
            solution = self.solve(new_board, new_pieces, new_constraints)
            if solution != False:
                return [move] + solution

        return False

This is following the exact same pattern as outlined above: generates new states for each of the legal moves, and continues exploring the new legal states one by one. If the solution has been found - the current move would be added to the solution. If not - the search continues until exhaustion.

legal_moves is missing, so let’s implement it next. What it has to do is for each piece in the pieces list generate a new state (board, remaining pieces) as if we made the move. Constraints don’t really change, so we can return the same argument. As per above, it would need to return the quadruplet: (move, new_board, new_pieces, constraints).

    def legal_moves(self, board, pieces, constraints):
        return (move for move in self.all_moves(board, pieces, constraints) if self.is_legal(move[1], constraints))

Here a generator expression is used to avoid having to store all possible moves in memory at once as search space is explored at each recursion depth. Instead the first matching value will be generated, the generator will return, search will continue in the deeper search level.

Subsequently, all_moves() can be defined as:

    def all_moves(self, board, pieces, constraints):
        """ Attempt to put one of available pieces into the available spaces on the board """
        free_cells = [(c[0], c[1]) for c in board if c[2] == 0]
        return (
            ((row, column, piece), new_board, new_pieces, constraints)
            for (row, column) in free_cells
            for piece in pieces
            for (new_board, new_pieces, new_constraints) in [self.perform_move((row, column, piece), board, pieces, constraints)]
        )

All it does is it attempts to place one of the available pieces into one of the free cells on the board.

When making a move, the selected piece is no longer available in the pieces list for further use. Instead it’s placed into the board matrix at given coordinates, making it permanent for deeper recursion to work with.

    def perform_move(self, move, board, pieces, constraints):
        """ Moves the given piece to the location on the board """
        new_pieces = pieces.copy()
        new_pieces.remove(move[2])

        new_board = board.copy()
        new_board.remove((move[0], move[1], 0))
        new_board.append(move)

        return new_board, new_pieces, constraints

Next let’s take care of is_legal(), which evaluates whether a given board is legal:

    def is_legal(self, board, constraints):
        """
        Is the board legal.
        - Rows and columns contain no duplicates
        - If there are constraints and all cells are filled in a given column - the sum of the column does not exceed the constraint
        - If all cells are filled in - constraint matches
        """

        lines = self.rows(board) + self.columns(board)

        no_duplicates = all(self.all_unique(self.filled_cells(line)) for line in lines)
        satisfies_constraints = all(self.satisfies_constraint(board, c) for c in constraints)

        return no_duplicates and satisfies_constraints

The uniqueness constraint in rows and columns:

    def all_unique(self, line):
        return len(line) == len(set(line))

    def rows(self, board):
        return self._lines(board, 0)

    def columns(self, board):
        return self._lines(board, 1)

    def _lines(self, board, dimension=0):
        discriminator = lambda c: c[dimension]
        cells = sorted(board, key=discriminator)
        groups = itertools.groupby(cells, key=discriminator)
        return [[c[2] for c in group] for index, group in groups]

    def filled_cells(self, line):
        return [x for x in line if x != 0]

The end goal of the summing constraint is to make sure that once all cells are filled in a line that the target sum is reached. However, in order for us to perform the search there will be times when some cells are not filled in. In such cases we’ll consider the constraint satisfied only if the sum of a line is lower than the target sum - there’s no point in continuing the search if we already blew over the limit.

    def satisfies_constraint(self, board, constraint):
        (dimension, element, target_sum) = constraint
        line = self._lines(board, dimension)[element]
        line_sum = sum(line)
        return (
            (line_sum == target_sum and self.all_cells_filled(line))
            or
            (line_sum < target_sum)
        )

That’s it!

And that’s it! We should have a working solver for the puzzle. Of course, having tests would be good to make sure it actually works and keeps on working, and I’ve already done that in the project’s repo.

Now we can test it out with the first level:

solver = Solver()
board = [
    (0, 1, 1),
    (1, 0, 0),
    (1, 1, 0),
    (2, 0, 2)
]
pieces = [1, 2]

moves = list(solver.solve(board, pieces, []))
print(moves)

# > [(1, 0, 1), (1, 1, 2)]

Or the third level:

solver = Solver()
board = [
    (0, 0, 0),
    (0, 2, 0),
    (0, 4, 5),
    (1, 1, 4),
    (1, 3, 0),
    (2, 0, 6),
    (2, 4, 0),
    (3, 1, 0),
    (3, 3, 6),
    (4, 0, 5),
    (4, 2, 4),
    (4, 4, 0),
]
pieces = [4, 5, 6, 4, 5, 6]

moves = list(solver.solve(board, pieces, []))
print(moves)

# > [(0, 0, 4), (0, 2, 6), (1, 3, 5), (2, 4, 4), (3, 1, 5), (4, 4, 6)]

Looks like it works! While this is not a very elegant approach, a brute force approach with small numbers still seems sufficient, which is great for the toy application. In the next post I’ll start looking into the computer vision part.

If you’d like to see the full code of the solver, you can find it on the project’s Github repo: puzbot - solver.py.