This post shows how Microsoft’s Z3 Theorem prover can be used to solve the Puzlogic puzzle game. We will replace the previous brute-force approach used in my puzlogic-bot with one that uses Z3.

Over last few posts we walked through building up puzlogic-bot: building the basic solver, the vision component using OpenCV, hooking up mouse controls with Pynput. As I’m learning to use Z3, the Z3 puzzle solver implementation would be an interesting practical exercise.

TL;DR: you can find the final solver code on Github.

Z3 is a theorem prover made by Microsoft. The SMT (Satisfiability modulo theories) family of solvers build up on SAT (Boolean satisfiability problem) family of solvers, providing capabilities to deal with numbers, lists, bit vectors and so on, instead of just boolean formulas.

Puzlogic is a number-based puzzle game. The goal of the game is to insert all given numbers into the board such that all rows and columns have unique numbers, and where a target sum is given - the row or column sums up to a given value.

Basics of Z3

“SAT/SMT by Example” by Dennis Yurichev is a great book to help beginners pick up Z3, and it was the inspiration for this post.

At school we all worked through equation systems like:

3x + 2y - z = 1
2x - 2y + 4z = -2
-x + 0.5y - z = 0

Z3 can be thought of as a constraint solver. Given a set of constraints, it will try to find a set of variable values that satisfy the constraints. If it can find a valid set of values - it means the constraints (and thus the theorem) is satisfiable. If not - it is not satisfiable.

The most basic example given in Yurichev’s book is:

from z3 import *

x = Real('x')
y = Real('y')
z = Real('z')

s = Solver()
s.add(3*x + 2*y - z == 1)
s.add(2*x + 2*y + 4*z == -2)
s.add(-x + 0.5y - z == 0)
print(s.check())
print(s.model())

Executing it outputs:

sat
[z = -2, y = -2, x = 1]

Here each equation can be considered as a constraint: a sum of variable values have to sum up to a certain value, satisfying the equation. Z3 is way more powerful than that, as evident by Z3py reference, but for the Puzlogic puzzle this is actually sufficient.

What we need next is how to describe the given puzzle as a set of constraints for use in Z3.

Solving Puzlogic puzzles

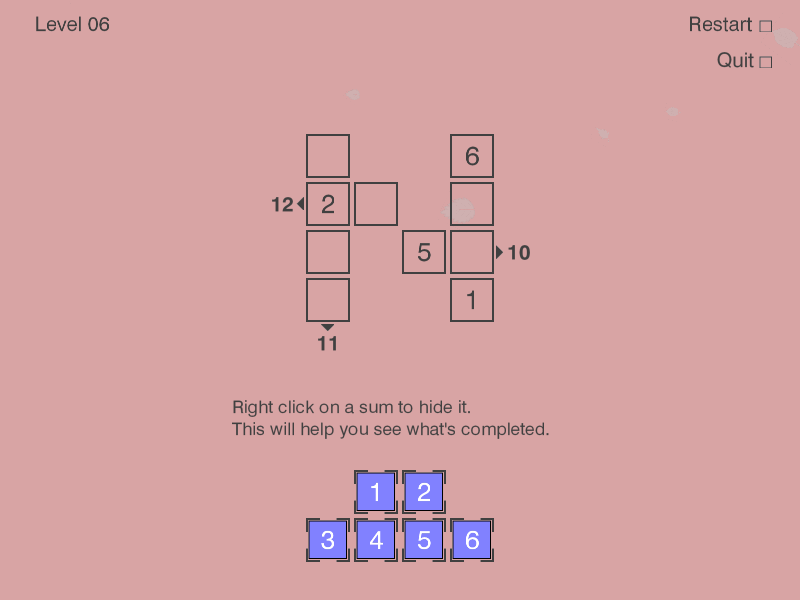
To quickly recap, the rules of the game are as follows:

• All numbers on a given row or column must be unique
• When a sum target is given for a given row or column, all cells in it must sum up to target sum
• All purple pieces at the bottom of the game board must be used to fill the game board

As established in the previous post, the game board is defined as a sparse matrix: a list of cells with x, y coordinates and a value. E.g.:

board = [
  # (row, column, value)
  (0, 0, 0),
  (0, 3, 6),
  (1, 0, 2),
  (1, 1, 0),
  (1, 3, 0),
  (2, 0, 0),
  (2, 2, 5),
  (2, 3, 0),
  (3, 0, 0),
  (3, 3, 1)
]

A value of zero is treated as an empty cell.

Purple game pieces are expressed just as a list of numbers: [1, 2, 3, 4, 5, 6].

While target sums can be expressed as (dimension, index, target_sum) tuples:

target_sums = [
  # (dimension, index, target_sum
  (0, 1, 12), # second row sums up to 12
  (0, 2, 10), # third row sums up to 10
  (1, 0, 11) # first column sums up to 11
]

Dimension of 0 marks a row, while 1 marks a column.

For the implementation there are 5 constraints to cover:

1. Limit values of pre-filled cells to the given values. Otherwise Z3 would assign them to some other values.
2. Allow empty cells to get values only of available pieces.
3. Require that there would be no duplicate values in any of the rows or columns.
4. If there are any sum targets specified for given rows or columns, require them to be satisfied.
5. Require that each purple game piece would be used only once.

0. Z3 variables

First, the board is extended by creating a Z3 variable for each cell to make it easier to apply constraints later on:

def cell_name(self, row, column):
  return 'c_%d_%d' % (row, column)

def solve(self):
  solver = Solver()

  # Create z3 variables for each cell
  extended_board = [(row, column, value, Int(self.cell_name(row, column))) for (row, column, value) in board]

Both default values and the purple game pieces are integers, hence the Int variable type.

1. Pre-filled variables

So far Z3 would be able to assign any integer to any of the variables we created so far. We will constrain the cells to use the already specified value where it is specified.

As mentioned before, in the board sparse matrix the value of 0 indicates an empty cell, so we initialize values for cells with values greater than 0:

def is_cell_empty(self, value):
  return value == 0

def set_prefilled_cell_values(self, board):
  return [cell == value for (_, _, value, cell) in board if not self.is_cell_empty(value)]

The cell == value is going to generate an expression object of type z3.z3.BoolRef, as cell here is a variable we created above with type Int, and value is a constant.

E.g. for the cell (0, 3, 6) the expression would be Int('c_0_3') == 6).

2. Empty cells can gain a value from any of the pieces

Having available pieces [1, 2, 3, 4, 5, 6], we want the following constraint for each of the empty cells: cell == 1 OR cell == 2 OR cell == 3 OR cell == 4 OR cell == 5 OR cell == 6

def set_possible_target_cell_values(self, board, pieces):
  constraints = []

  for (row, column, value, cell) in board:
    if self.is_cell_empty(value):
      any_of_the_piece_values = [cell == piece for piece in pieces]
      constraints.append(Or(*any_of_the_piece_values))

  return constraints

This returns a list of constraints in the format:

constraints = [
  Or(c_0_0 == 1, c_0_0 == 2, c_0_0 == 3, c_0_0 == 4, c_0_0 == 5, c_0_0 == 6),
  Or(c_1_1 == 1, c_1_1 == 2, c_1_1 == 3, c_1_1 == 4, c_1_1 == 5, c_1_1 == 6),
  # ...
]

You may notice that this allows cells on the same row or column to have a common value. This will be fixed by constraint 3. This also allows the same piece to be used in multiple cells, we’ll fix it with constraint 4.

3. No duplicates in rows or columns

def require_unique_row_and_column_cells(self, board):
  return [
    c1 != c2
      for ((x1, y1, _, c1), (x2, y2, _, c2)) in itertools.combinations(board, 2)
      if x1 == x2 or y1 == y2]

itertools.combinations(), given a list of [A, B, C, ...] will output combinations [AB, AC, BC, ...] without repetitions. E.g. c_0_0 != c_0_3, c_0_0 != c_1_0, c_0_0 != c_2_0 and so on.

We use it to make sure that no cells with a common row or column index have the same value. Instead of manually iterating over each cell combination, we could’ve used Distinct(args) expression for each row and column.

4. Satisfying sum targets

Any column or row may have a sum target that its pieces should sum up to.

  def match_sum_requirements(self, board, sum_requirements):
    constraints = []
    for (dimension, index, target_sum) in sum_requirements:
      relevant_cells = [cell[3] for cell in board if cell[dimension] == index]
      constraints.append(sum(relevant_cells) == target_sum)

    return constraints

It’s a fairly straightforward sum of relevant cells. E.g. for the (0, 1, 12) sum target, the constraint expression would be Sum(c_1_0, c_1_1, c_1_3) == 12

5. All pieces are used once

Here that can be ensured by summing up pieces used in empty cells, and it should match the sum of pieces given originally. Just checking for unique values is insufficient, as on some levels there may be multiple pieces with the same value, e.g. [4, 5, 6, 4, 5, 6].

  def target_cells_use_all_available_pieces(self, board, pieces):
    empty_cells = [cell for (_, _, value, cell) in board if self.is_cell_empty(value)]
    return [sum(empty_cells) == sum(pieces)]

Putting it all together

Now that we have methods that generate constraint expressions, we can add them all to the solver and format the output to make it look more readable:

constraints = \
  self.set_prefilled_cell_values(extended_board) + \
  self.set_possible_target_cell_values(extended_board, pieces) + \
  self.require_unique_row_and_column_cells(extended_board) + \
  self.match_sum_requirements(extended_board, sum_requirements) + \
  self.target_cells_use_all_available_pieces(extended_board, pieces)

for constraint in constraints:
  solver.add(constraint)

if solver.check() == sat:
  model = solver.model()
  return [
    (row, column, model[cell].as_long())
      for (row, column, value, cell) in extended_board
      if self.is_cell_empty(value)
  ]
else:
  return False

It’s worth noting that solver.check() may return either z3.sat or z3.unsat. If it is satisfiable, solver.model() will contain a list of values:

# solver.model()
[c_1_1 = 6,
 c_3_0 = 5,
 c_2_3 = 2,
 c_1_3 = 4,
 c_0_0 = 1,
 c_2_0 = 3,
 c_3_3 = 1,
 c_2_2 = 5,
 c_1_0 = 2,
 c_0_3 = 6]

The values, however, are still Z3 objects, so e.g. an Int() object value may need to be converted into a primitive int via as_long() method.

Once a model is solved, we also nicely format the return values in the form of:

solution = [
  # (row, column, expected_piece_value)
  (0, 0, 1),
  (1, 1, 6),
  (1, 3, 4),
  (2, 0, 3),
  (2, 3, 2),
  (3, 0, 5)
]

The steps, if done by the human, will solve the puzzle.

The final set of constraints for level 6 was:

[
  # 1. Pre-filled cell values
  c_0_3 == 6, c_1_0 == 2, c_2_2 == 5, c_3_3 == 1,

  # 2. Possible values for empty cells
  Or(c_0_0 == 1, c_0_0 == 2, c_0_0 == 3, c_0_0 == 4, c_0_0 == 5, c_0_0 == 6),
  Or(c_1_1 == 1, c_1_1 == 2, c_1_1 == 3, c_1_1 == 4, c_1_1 == 5, c_1_1 == 6),
  Or(c_1_3 == 1, c_1_3 == 2, c_1_3 == 3, c_1_3 == 4, c_1_3 == 5, c_1_3 == 6),
  Or(c_2_0 == 1, c_2_0 == 2, c_2_0 == 3, c_2_0 == 4, c_2_0 == 5, c_2_0 == 6),
  Or(c_2_3 == 1, c_2_3 == 2, c_2_3 == 3, c_2_3 == 4, c_2_3 == 5, c_2_3 == 6),
  Or(c_3_0 == 1, c_3_0 == 2, c_3_0 == 3, c_3_0 == 4, c_3_0 == 5, c_3_0 == 6),

  # 3. Unique values in rows and columns
  c_0_0 != c_0_3, c_0_0 != c_1_0, c_0_0 != c_2_0, c_0_0 != c_3_0,
  c_0_3 != c_1_3, c_0_3 != c_2_3, c_0_3 != c_3_3,
  c_1_0 != c_1_1, c_1_0 != c_1_3, c_1_0 != c_2_0, c_1_0 != c_3_0,
  c_1_1 != c_1_3,
  c_1_3 != c_2_3, c_1_3 != c_3_3,
  c_2_0 != c_2_2, c_2_0 != c_2_3, c_2_0 != c_3_0,
  c_2_2 != c_2_3,
  c_2_3 != c_3_3,
  c_3_0 != c_3_3,

  # 4. Row/column sum targets
  0 + c_1_0 + c_1_1 + c_1_3 == 12,
  0 + c_2_0 + c_2_2 + c_2_3 == 10,
  0 + c_0_0 + c_1_0 + c_2_0 + c_3_0 == 11,

  # 5. Ensuring that all pieces have been used once
  0 + c_0_0 + c_1_1 + c_1_3 + c_2_0 + c_2_3 + c_3_0 == 21
]

Final thoughts

The puzlogic-bot project is able to use the Z3 based solver for first few levels, but that’s only because the Vision component is not able to read the row/column target sums correctly. As we have seen in the example, the Z3-based solver has no issues dealing with target sums in further levels.

I found it rather surprising just how approachable Z3 was for a newbie. The puzzle problem perhaps was primitive, but the only difficulty was to not get lost in the constraint definitions the puzzle required.

You can find the final code of the solver on Github. If you are curious how puzlogic-bot was built, I have a series of posts on it too.

How do you use or would use constraint solvers?