Last time we briefly looked over resources for learning TLA+ and PlusCal, as well as wrote a basic spec to prove equivalence of a few logic formulas. In this post I thought it would be interesting to write a spec for a more common scenario.

The idea

This is inspired by the issue we had with MailPoet 2. An attacker was able to successfully continuously sign up users, the users would get sent a subscription confirmation email with each subscription, that way some email addresses were effectively bombed with emails. Let’s try to model and explore this situation.

In the actual system we have the client, server, emails being sent out, network connections… Lots of details, most of them we can probably ignore safely and still model the system sufficiently.

Sending messages without any rate-limiting

Let’s start with the initial situation: we want to allow TLC to send arbitrary “Messages” (actual content, metadata is irrelevant here) over time, and we want to put some limit on how many messages can be sent out over some period of time.

For a start we’ll model just a single sender, storing messages in a set as a log, noting their contents and time when they were sent. Contents would be irrelevant, but in this case it helps humans interpret the situation. We’ll allow TLC to keep sending an arbitrary number of messages one by one, and then increment the time. That way we allow our model to “send 60 messages in one second”.

Finally, we add an invariant to make sure that the number of messages sent in one second does not go over the limit. Here’s the code:

----------------------------- MODULE Throttling -----------------------------
EXTENDS Naturals, FiniteSets
CONSTANTS Window, Limit, MaxTime

(* --algorithm throttling
variables
    Time = 0,
    MessageId = 0,
    MessageLog = {};

macro SendMessage(Message)
begin
    MessageLog := MessageLog \union {[Time |-> Time, Message |-> Message]};
end macro;

begin
    Simulate:
    while Time < MaxTime do
        either
            SendMessage:
                SendMessage(MessageId);
                MessageId := MessageId + 1;
        or
            TimeStep:
                Time := Time + 1;
        end either;
    end while;
end algorithm; *)

FrequencyInvariant ==
    \A T \in 0..MaxTime: (Cardinality({Message \in MessageLog: Message["Time"] = T}) <= Limit)

The individual log in MessageLog is a record with 2 keys: Time and Message, and the MessageLog itself is a set. The FrequencyInvariant invariant checks that during every second of our simulation the number of messages sent does not exceed our Limit.

We’ll use these constant values for our initial runs:

Window <- 3
MaxTime <- 5
Limit <- 3

If we translate the PlusCal code to TLA+ (with Ctrl+T in Toolbox) and run the model with TLC, as we expected - it quickly finds an error:

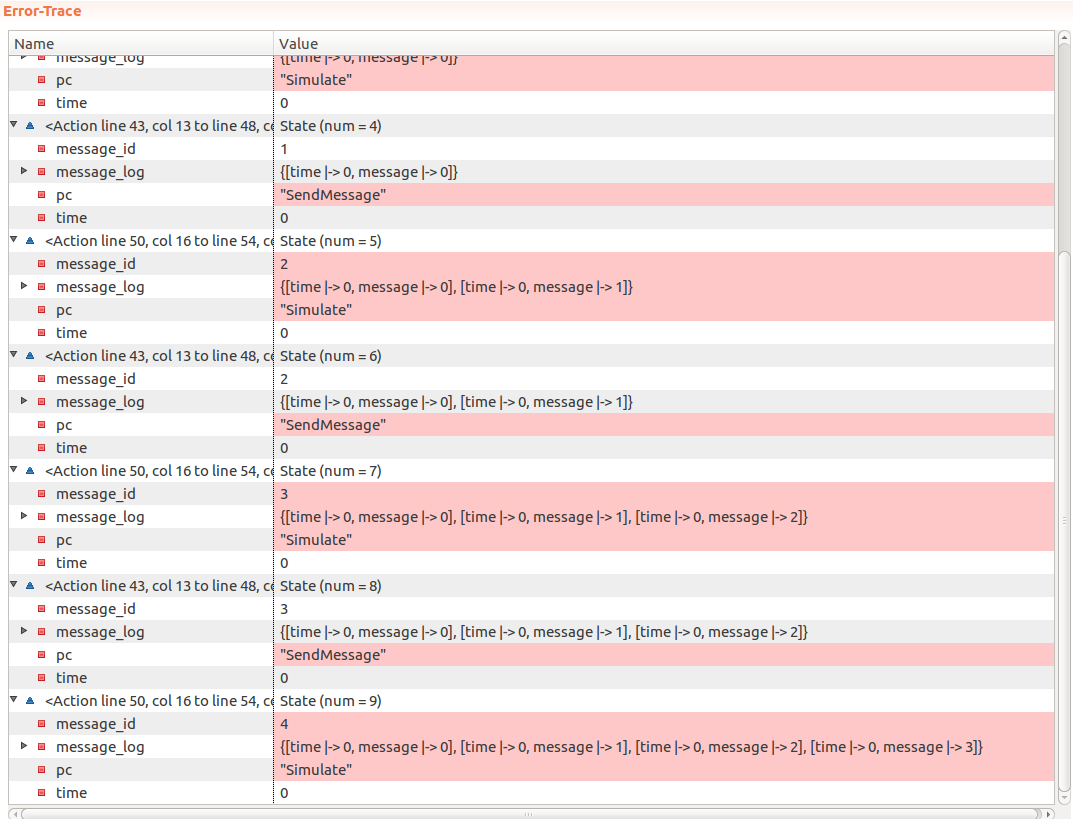
Since we did not perform any throttling and instead allowed TLC to “send” an arbitrary number of messages - TLC sent 4 messages before the invariant failed.

Time based throttling

As the next step let’s make use of the Window constant and alter SendMessage() macro to accept messages only if doing so does not exceed our Limit.

First of all, given a Time, we want to grab a set of times falling within our window. So if the current Time = 5, and our Window = 2, we want it to return {3, 4, 5}:

define
  GetTimeWindow(T) ==
      {X \in Nat : X <= T /\ X >= (T - Window)}
\* ...

Next, we want to define a way to count the number of messages sent over a set of specific times. So if our time window is {3, 4, 5, 6}, we count the total number of messages sent at Time = 3, Time = 4, …, Time = 6:

\* ...
    SentMessages(TimeWindow) ==
            Cardinality({Message \in MessageLog: Message.Time \in TimeWindow})
end define;

Then we can write a ThrottledSendMessage variant of the SendMessage macro:

macro ThrottledSendMessage(Message)
begin
    if SentMessages(GetTimeWindow(Time)) < Limit then
        SendMessage(Message);
    end if;
end macro;

Here we silently drop the overflow messages, “sending” only what’s within the limit. At this point this is the code we have:

----------------------------- MODULE Throttling -----------------------------
EXTENDS Naturals, FiniteSets
CONSTANTS Window, Limit, MaxTime

(* --algorithm throttling
variables
    Time = 0,
    MessageId = 0,
    MessageLog = {};   

define
    GetTimeWindow(T) ==
        {X \in Nat : X <= T /\ X >= (T - Window)}
        
    SentMessages(TimeWindow) ==
        Cardinality({Message \in MessageLog: Message.Time \in TimeWindow})
end define;   
 
macro SendMessage(Message)
begin
    MessageLog := MessageLog \union {[Time |-> Time, Message |-> Message]};
end macro;

macro ThrottledSendMessage(Message)
begin   
    if SentMessages(GetTimeWindow(Time)) < Limit then
        SendMessage(Message);
    end if;
end macro;
     
begin
    Simulate:
    while Time < MaxTime do
        either
            SendMessage:
                ThrottledSendMessage(MessageId);
                MessageId := MessageId + 1;
        or
            TimeStep:
                Time := Time + 1;
        end either;
    end while;    
end algorithm; *)

FrequencyInvariant ==
    \A T \in 0..MaxTime: (Cardinality({Message \in MessageLog: Message["Time"] = T}) <= Limit)

=============================================================================

At this point we can run our model:

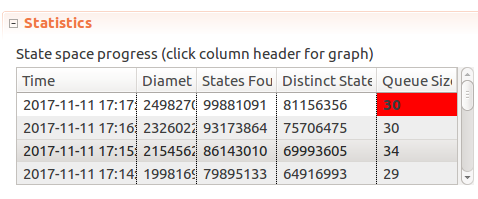
And hmm… After 10-20 minutes of checking TLC does not finish, the number of distinct states keeps going up. I even tried reducing our constants to Window <- 2, MaxTime <- 3, Limit <- 3. As TLC started climbing over 2GB of memory used I cancelled the process. Now what?

Assuming that the process could never terminate, what could cause that? We tried to limit our “simulation” to MaxTime <- 3, time keeps moving on, number of messages “sent” is capped by Limit. But looking back at the SendMessage label, ThrottledSendMessage() gets called and it’s result isn’t considered. But regardless of whether or not a message has been sent, MessageId always keeps going up, and each such new state could mean TLC needs to keep going. So that’s the hypothesis.

Let’s try capping that by moving MessageId := MessageId + 1; from SendMessage label to ThrottledSendMessage macro, and perform it only if the message is successfully sent. Now if we rerun the model:

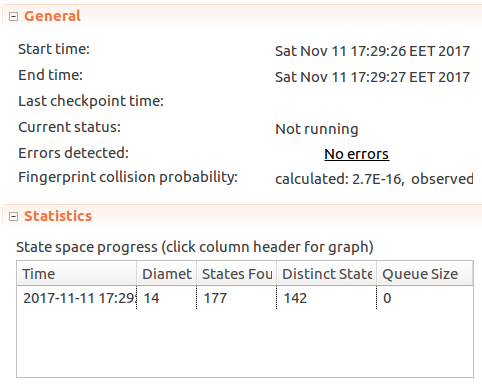
We can see that TLC has found no errors, TLC found 142 distinct states and the number of messages sent at any single Time value hasn’t exceeded Limit <- 3. Great!

Next let’s strengthen the FrequencyInvariant. Right now it checks whether the number of messages sent at ONE SPECIFIC VALUE OF Time does not exceed the Limit. But we want to ensure that the same holds for the whole Window of time values:

FrequencyInvariant ==
    \A T \in 0..MaxTime: SentMessages(GetTimeWindow(T)) <= Limit

And because the spec already had implemented time-window based rate limiting - the number of states checked stayed the same:

At this point running TLC with smaller model sizes helped build confidence in the model. But will it hold if we crank up constants to say… Window <- 5, MaxTime <- 30, Limit <- 10? Unfortunately in an hour of running the model the number of distinct states and queue size just kept going up at a consistent pace, so after it consumed over 1gb of memory it had to be terminated.

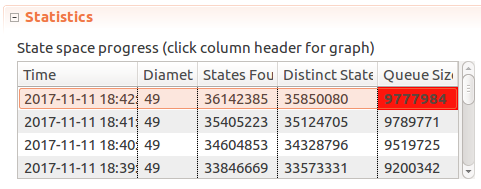
I think Limit being high creates quite a few states, as you can spread out 10 messages over 5 distinct times in 5^10 ways. Spread that out over 30-5+1=26 possible windows, bringing us into hundreds of millions of possible states. The number of states quickly goes up even in this fairly simple case! It took my laptop ~10 minutes to explore ~13 million states reached with Window <- 5, MaxTime <- 15, Limit < 5 configuration:

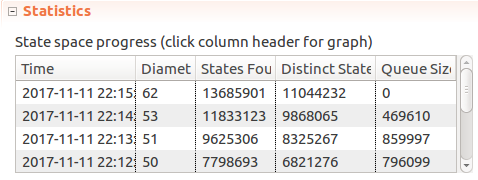
For the sake of the example that’s probably sufficient. I don’t see any point in checking larger models in this case, but on a faster computer, or on a distributed set of servers it could be checked much faster. Yes - TLC does work in a distributed mode, which could be an interesting feature to play around in itself.